3 \(M_1\) 
\(M_2\) 
\(M_3\) 
| Acceptance problem | ||
| for Turing machines | \(A_{TM}\) | \(\{ \langle M,w \rangle \mid \text{$M$ is a Turing machine that accepts input string $w$}\}\) |
| Language emptiness testing | ||
| for Turing machines | \(E_{TM}\) | \(\{ \langle M \rangle \mid \text{$M$ is a Turing machine and $L(M) = \emptyset$\}}\) |
| Language equality testing | ||
| for Turing machines | \(EQ_{TM}\) | \(\{ \langle M_1, M_2 \rangle \mid \text{$M_1$ and $M_2$ are Turing machines and $L(M_1) =L(M_2)$\}}\) |
3 \(M_1\)
\(M_2\)
\(M_3\)
Example strings in \(A_{TM}\)
Example strings in \(E_{TM}\)
Example strings in \(EQ_{TM}\)
Theorem: \(A_{TM}\) is Turing-recognizable.
Strategy: To prove this theorem, we need to define a Turing machine \(R_{ATM}\) such that \(L(R_{ATM}) = A_{TM}\).
Define \(R_{ATM} =\) “
Proof of correctness:
We will show that \(A_{TM}\) is undecidable. First, let’s explore what that means.
To prove that a computational problem is decidable, we find/ build a Turing machine that recognizes the language encoding the computational problem, and that is a decider.
How do we prove a specific problem is not decidable?
How would we even find such a computational problem?
Counting arguments for the existence of an undecidable language:
The set of all Turing machines is countably infinite.
Each recognizable language has at least one Turing machine that recognizes it (by definition), so there can be no more Turing-recognizable languages than there are Turing machines.
Since there are infinitely many Turing-recognizable languages (think of the singleton sets), there are countably infinitely many Turing-recognizable languages.
Such the set of Turing-decidable languages is an infinite subset of the set of Turing-recognizable languages, the set of Turing-decidable languages is also countably infinite.
Since there are uncountably many languages (because \(\mathcal{P}(\Sigma^*)\) is uncountable), there are uncountably many unrecognizable languages and there are uncountably many undecidable languages.
Thus, there’s at least one undecidable language!
What’s a specific example of a language that is unrecognizable or undecidable?
To prove that a language is undecidable, we need to prove that there is no Turing machine that decides it.
Key idea: proof by contradiction relying on self-referential disagreement.
Theorem: \(A_{TM}\) is not Turing-decidable.
Proof: Suppose towards a contradiction that there is a Turing machine that decides \(A_{TM}\). We call this presumed machine \(M_{ATM}\).
By assumption, for every Turing machine \(M\) and every string \(w\)
If \(w \in L(M)\), then the computation of \(M_{ATM}\) on \(\langle M,w \rangle ~~ \underline{\phantom{\hspace{2.5in}}}\)
If \(w \notin L(M)\), then the computation of \(M_{ATM}\) on \(\langle M,w \rangle ~~ \underline{\phantom{\hspace{2.5in}}}\)
Define a new Turing machine using the high-level description:
\(D =\)“ On input \(\langle M \rangle\), where \(M\) is a Turing machine:
Run \(M_{ATM}\) on \(\langle M, \langle M \rangle \rangle\).
If \(M_{ATM}\) accepts, reject; if \(M_{ATM}\) rejects, accept."
Is \(D\) a Turing machine?
Is \(D\) a decider?
What is the result of the computation of \(D\) on \(\langle D \rangle\)?
Definition: A language \(L\) over an alphabet \(\Sigma\) is called co-recognizable if its complement, defined as \(\Sigma^* \setminus L = \{ x \in \Sigma^* \mid x \notin L \}\), is Turing-recognizable.
Theorem (Sipser Theorem 4.22): A language is Turing-decidable if and only if both it and its complement are Turing-recognizable.
Proof, first direction: Suppose language \(L\) is Turing-decidable. WTS that both it and its complement are Turing-recognizable.
Proof, second direction: Suppose language \(L\) is Turing-recognizable, and so is its complement. WTS that \(L\) is Turing-decidable.
Notation: The complement of a set \(X\) is denoted with a superscript \(c\), \(X^c\), or an overline, \(\overline{X}\).
These definitions are on pages 101-102.
| Term | Typical symbol | Meaning |
| or Notation | ||
| Context-free grammar (CFG) | \(G\) | \(G = (V, \Sigma, R, S)\) |
| The set of variables | \(V\) | Finite set of symbols that represent phases in production pattern |
| The set of terminals | \(\Sigma\) | Alphabet of symbols of strings generated by CFG |
| \(V \cap \Sigma = \emptyset\) | ||
| The set of rules | \(R\) | Each rule is \(A \to u\) with \(A \in V\) and \(u \in (V \cup \Sigma)^*\) |
| The start variable | \(S\) | Usually on left-hand-side of first/ topmost rule |
| Derivation | \(S \Rightarrow \cdots \Rightarrow w\) | Sequence of substitutions in a CFG (also written \(S \Rightarrow^* w\)). At each step, we can apply one rule to one occurrence of a variable in the current string by substituting that occurrence of the variable with the right-hand-side of the rule. The derivation must end when the current string has only terminals (no variables) because then there are no instances of variables to apply a rule to. |
| Language generated by the context-free grammar \(G\) | \(L(G)\) | The set of strings for which there is a derivation in \(G\). Symbolically: \(\{ w \in \Sigma^* \mid S \Rightarrow^* w \}\) i.e. \[\{ w \in \Sigma^* \mid \text{there is derivation in $G$ that ends in $w$} \}\] |
| Context-free language | A language that is the language generated by some context-free grammar |
Examples of context-free grammars, derivations in those grammars, and the languages generated by those grammars
\(G_1 = (\{S\}, \{0\}, R, S)\) with rules \[\begin{aligned} &S \to 0S\\ &S \to 0\\ \end{aligned}\] In \(L(G_1)\) …
Not in \(L(G_1)\) …
\(G_2 = (\{S\}, \{0,1\}, R, S)\) \[S \to 0S \mid 1S \mid \varepsilon\] In \(L(G_2)\) …
Not in \(L(G_2)\) …
\((\{S, T\}, \{0, 1\}, R, S)\) with rules \[\begin{aligned} &S \to T1T1T1T \\ &T \to 0T \mid 1T \mid \varepsilon \end{aligned}\]
In \(L(G_3)\) …
Not in \(L(G_3)\) …
\(G_4 = (\{A, B\}, \{0, 1\}, R, A)\) with rules \[A \to 0A0 \mid 0A1 \mid 1A0 \mid 1A1 \mid 1\] In \(L(G_4)\) …
Not in \(L(G_4)\) …
Design a CFG to generate the language \(\{a^n b^n \mid n \geq 0\}\)
Sample derivation:
Warmup: Design a CFG to generate the language \(\{a^i b^j \mid j \geq i \geq 0\}\)
Sample derivation:
Design a PDA to recognize the language \(\{a^i b^j \mid j \geq i \geq 0\}\)
Theorem 2.20: A language is generated by some context-free grammar if and only if it is recognized by some push-down automaton.
Definition: a language is called context-free if it is the language generated by a context-free grammar. The class of all context-free language over a given alphabet \(\Sigma\) is called CFL.
Consequences:
Quick proof that every regular language is context free
To prove closure of the class of context-free languages under a given operation, we can choose either of two modes of proof (via CFGs or PDAs) depending on which is easier
To fully specify a PDA we could give its \(6\)-tuple formal definition or we could give its input alphabet, stack alphabet, and state diagram. An informal description of a PDA is a step-by-step description of how its computations would process input strings; the reader should be able to reconstruct the state diagram or formal definition precisely from such a descripton. The informal description of a PDA can refer to some common modules or subroutines that are computable by PDAs:
PDAs can “test for emptiness of stack” without providing details. How? We can always push a special end-of-stack symbol, \(\$\), at the start, before processing any input, and then use this symbol as a flag.
PDAs can “test for end of input” without providing details. How? We can transform a PDA to one where accepting states are only those reachable when there are no more input symbols.
Suppose \(L_1\) and \(L_2\) are context-free languages over \(\Sigma\). Goal: \(L_1 \cup L_2\) is also context-free.
Approach 1: with PDAs
Let \(M_1 = ( Q_1, \Sigma, \Gamma_1, \delta_1, q_1, F_1)\) and \(M_2 = ( Q_2, \Sigma, \Gamma_2, \delta_2, q_2, F_2)\) be PDAs with \(L(M_1) = L_1\) and \(L(M_2) = L_2\).
Define \(M =\)
Approach 2: with CFGs
Let \(G_1 = (V_1, \Sigma, R_1, S_1)\) and \(G_2 = (V_2, \Sigma, R_2, S_2)\) be CFGs with \(L(G_1) = L_1\) and \(L(G_2) = L_2\).
Define \(G =\)
Suppose \(L_1\) and \(L_2\) are context-free languages over \(\Sigma\). Goal: \(L_1 \circ L_2\) is also context-free.
Approach 1: with PDAs
Let \(M_1 = ( Q_1, \Sigma, \Gamma_1, \delta_1, q_1, F_1)\) and \(M_2 = ( Q_2, \Sigma, \Gamma_2, \delta_2, q_2, F_2)\) be PDAs with \(L(M_1) = L_1\) and \(L(M_2) = L_2\).
Define \(M =\)
Approach 2: with CFGs
Let \(G_1 = (V_1, \Sigma, R_1, S_1)\) and \(G_2 = (V_2, \Sigma, R_2, S_2)\) be CFGs with \(L(G_1) = L_1\) and \(L(G_2) = L_2\).
Define \(G =\)
Summary
Over a fixed alphabet \(\Sigma\), a language \(L\) is regular
iff it is described by some regular expression
iff it is recognized by some DFA
iff it is recognized by some NFA
Over a fixed alphabet \(\Sigma\), a language \(L\) is context-free
iff it is generated by some CFG
iff it is recognized by some PDA
Fact: Every regular language is a context-free language.
Fact: There are context-free languages that are not nonregular.
Fact: There are countably many regular languages.
Fact: There are countably inifnitely many context-free languages.
Consequence: Most languages are not context-free!
Examples of non-context-free languages
\[\begin{aligned} &\{ a^n b^n c^n \mid 0 \leq n , n \in \mathbb{Z}\}\\ &\{ a^i b^j c^k \mid 0 \leq i \leq j \leq k , i \in \mathbb{Z}, j \in \mathbb{Z}, k \in \mathbb{Z}\}\\ &\{ ww \mid w \in \{0,1\}^* \} \end{aligned}\] (Sipser Ex 2.36, Ex 2.37, 2.38)
There is a Pumping Lemma for CFL that can be used to prove a specific language is non-context-free: If \(A\) is a context-free language, there there is a number \(p\) where, if \(s\) is any string in \(A\) of length at least \(p\), then \(s\) may be divided into five pieces \(s = uvxyz\) where (1) for each \(i \geq 0\), \(uv^ixy^iz \in A\), (2) \(|uv|>0\), (3) \(|vxy| \leq p\). We will not go into the details of the proof or application of Pumping Lemma for CFLs this quarter.
Recap so far: In DFA, the only memory available is in the states. Automata can only “remember” finitely far in the past and finitely much information, because they can have only finitely many states. If a computation path of a DFA visits the same state more than once, the machine can’t tell the difference between the first time and future times it visits this state. Thus, if a DFA accepts one long string, then it must accept (infinitely) many similar strings.
Definition A positive integer \(p\) is a pumping length of a language \(L\) over \(\Sigma\) means that, for each string \(s \in \Sigma^*\), if \(|s| \geq p\) and \(s \in L\), then there are strings \(x,y,z\) such that \[s = xyz\] and \[|y| > 0, \qquad \qquad \text{ for each $i \geq 0$, $xy^i z \in L$}, \qquad \text{and} \qquad \qquad |xy| \leq p.\]
Negation: A positive integer \(p\) is not a pumping length of a language \(L\) over \(\Sigma\) iff \[\exists s \left(~ |s| \geq p \wedge s \in L \wedge \forall x \forall y \forall z \left( ~\left( s = xyz \wedge |y| > 0 \wedge |xy| \leq p~ \right) \to \exists i ( i \geq 0 \wedge xy^iz \notin L ) \right) ~\right)\] Informally:
Restating Pumping Lemma: If \(L\) is a regular language, then it has a pumping length.
Contrapositive: If \(L\) has no pumping length, then it is nonregular.
The Pumping Lemma cannot be used to prove that a language is regular.
The Pumping Lemma can be used to prove that a language is not regular.
Extra practice: Exercise 1.49 in the book.
Proof strategy: To prove that a language \(L\) is not regular,
Consider an arbitrary positive integer \(p\)
Prove that \(p\) is not a pumping length for \(L\)
Conclude that \(L\) does not have any pumping length, and therefore it is not regular.
Example: \(\Sigma = \{0,1\}\), \(L = \{ 0^n 1^n \mid n \geq 0\}\).
Fix \(p\) an arbitrary positive integer. List strings that are in \(L\) and have length greater than or equal to \(p\):
Pick \(s =\)
Suppose \(s = xyz\) with \(|xy| \leq p\) and \(|y| > 0\).
Then when \(i = \hspace{1in}\), \(xy^i z = \hspace{1in}\)
Example: \(\Sigma = \{0,1\}\), \(L = \{w w^{\mathcal{R}} \mid w \in \{0,1\}^*\}\). Remember that the reverse of a string \(w\) is denoted \(w^\mathcal{R}\) and means to write \(w\) in the opposite order, if \(w = w_1 \cdots w_n\) then \(w^\mathcal{R} = w_n \cdots w_1\). Note: \(\varepsilon^\mathcal{R} = \varepsilon\).
Fix \(p\) an arbitrary positive integer. List strings that are in \(L\) and have length greater than or equal to \(p\):
Pick \(s =\)
Suppose \(s = xyz\) with \(|xy| \leq p\) and \(|y| > 0\).
Then when \(i = \hspace{1in}\), \(xy^i z = \hspace{1in}\)
Example: \(\Sigma = \{0,1\}\), \(L = \{0^j1^k \mid j \geq k \geq 0\}\).
Fix \(p\) an arbitrary positive integer. List strings that are in \(L\) and have length greater than or equal to \(p\):
Pick \(s =\)
Suppose \(s = xyz\) with \(|xy| \leq p\) and \(|y| > 0\).
Then when \(i = \hspace{1in}\), \(xy^i z = \hspace{1in}\)
Example: \(\Sigma = \{0,1\}\), \(L = \{0^n1^m0^n \mid m,n \geq 0\}\).
Fix \(p\) an arbitrary positive integer. List strings that are in \(L\) and have length greater than or equal to \(p\):
Pick \(s =\)
Suppose \(s = xyz\) with \(|xy| \leq p\) and \(|y| > 0\).
Then when \(i = \hspace{1in}\), \(xy^i z = \hspace{1in}\)
Extra practice:
| Language | \(s \in L\) | \(s \notin L\) | Is the language regular or nonregular? |
|---|---|---|---|
| \(\{a^nb^n \mid 0 \leq n \leq 5 \}\) | |||
| \(\{b^n a^n \mid n \geq 2\}\) | |||
| \(\{a^m b^n \mid 0 \leq m\leq n\}\) | |||
| \(\{a^m b^n \mid m \geq n+3, n \geq 0\}\) | |||
| \(\{b^m a^n \mid m \geq 1, n \geq 3\}\) | |||
| \(\{ w \in \{a,b\}^* \mid w = w^\mathcal{R} \}\) | |||
| \(\{ ww^\mathcal{R} \mid w\in \{a,b\}^* \}\) | |||
Draw the state diagram and give the formal definition of a PDA with \(\Sigma = \Gamma\).
Draw the state diagram and give the formal definition of a PDA with \(\Sigma \cap \Gamma = \emptyset\).
For the PDA state diagrams below, \(\Sigma = \{0,1\}\).
| Mathematical description of language | State diagram of PDA recognizing language |
|---|---|
| \(\Gamma = \{ \$, \#\}\) | |
 |
|
| \(\Gamma = \{ {@}, 1\}\) | |
 |
|
| \(\{ 0^i 1^j 0^k \mid i,j,k \geq 0 \}\) | |
Note: alternate notation is to replace \(;\) with \(\to\)
Big picture: PDAs were motivated by wanting to add some memory of unbounded size to NFA. How do we accomplish a similar enhancement of regular expressions to get a syntactic model that is more expressive?
DFA, NFA, PDA: Machines process one input string at a time; the computation of a machine on its input string reads the input from left to right.
Regular expressions: Syntactic descriptions of all strings that match a particular pattern; the language described by a regular expression is built up recursively according to the expression’s syntax
Context-free grammars: Rules to produce one string at a time, adding characters from the middle, beginning, or end of the final string as the derivation proceeds.
We are ready to introduce a formal model that will capture a notion of general purpose computation.
Similar to DFA, NFA, PDA: input will be an arbitrary string over a fixed alphabet.
Different from NFA, PDA: machine is deterministic.
Different from DFA, NFA, PDA: read-write head can move both to the left and to the right, and can extend to the right past the original input.
Similar to DFA, NFA, PDA: transition function drives computation one step at a time by moving within a finite set of states, always starting at designated start state.
Different from DFA, NFA, PDA: the special states for rejecting and accepting take effect immediately.
(See more details: Sipser p. 166)
Formally: a Turing machine is \(M= (Q, \Sigma, \Gamma, \delta, q_0, q_{accept}, q_{reject})\) where \(\delta\) is the transition function \[\delta: Q\times \Gamma \to Q \times \Gamma \times \{L, R\}\] The computation of \(M\) on a string \(w\) over \(\Sigma\) is:
Read/write head starts at leftmost position on tape.
Input string is written on \(|w|\)-many leftmost cells of tape, rest of the tape cells have the blank symbol. Tape alphabet is \(\Gamma\) with \(\textvisiblespace\in \Gamma\) and \(\Sigma \subseteq \Gamma\). The blank symbol \(\textvisiblespace \notin \Sigma\).
Given current state of machine and current symbol being read at the tape head, the machine transitions to next state, writes a symbol to the current position of the tape head (overwriting existing symbol), and moves the tape head L or R (if possible).
Computation ends if and when machine enters either the accept or the reject state. This is called halting. Note: \(q_{accept} \neq q_{reject}\).
The language recognized by the Turing machine \(M\), is \(L(M) = \{ w \in \Sigma^* \mid w \textrm{ is accepted by } M\}\), which is defined as \[\{ w \in \Sigma^* \mid \textrm{computation of $M$ on $w$ halts after entering the accept state}\}\]
2 
Formal definition:
Sample computation:
| \(q0\downarrow\) | ||||||
|---|---|---|---|---|---|---|
| \(0\) | \(0\) | \(0\) | \(\textvisiblespace\) | \(\textvisiblespace\) | \(\textvisiblespace\) | \(\textvisiblespace\) |
The language recognized by this machine is …
Describing Turing machines (Sipser p. 185) To define a Turing machine, we could give a
Formal definition: the \(7\)-tuple of parameters including set of states, input alphabet, tape alphabet, transition function, start state, accept state, and reject state; or,
Implementation-level definition: English prose that describes the Turing machine head movements relative to contents of tape, and conditions for accepting / rejecting based on those contents.
High-level description: description of algorithm (precise sequence of instructions), without implementation details of machine. As part of this description, can “call" and run another TM as a subroutine.
Fix \(\Sigma = \{0,1\}\), \(\Gamma = \{ 0, 1, \textvisiblespace\}\) for the Turing machines with the following state diagrams:
Example of string accepted:
Example of string rejected:
Implementation-level description
High-level description
Example of string accepted:
Example of string rejected:
Implementation-level description
High-level description
Example of string accepted:
Example of string rejected:
Implementation-level description
High-level description
Example of string accepted:
Example of string rejected:
Implementation-level description
High-level description
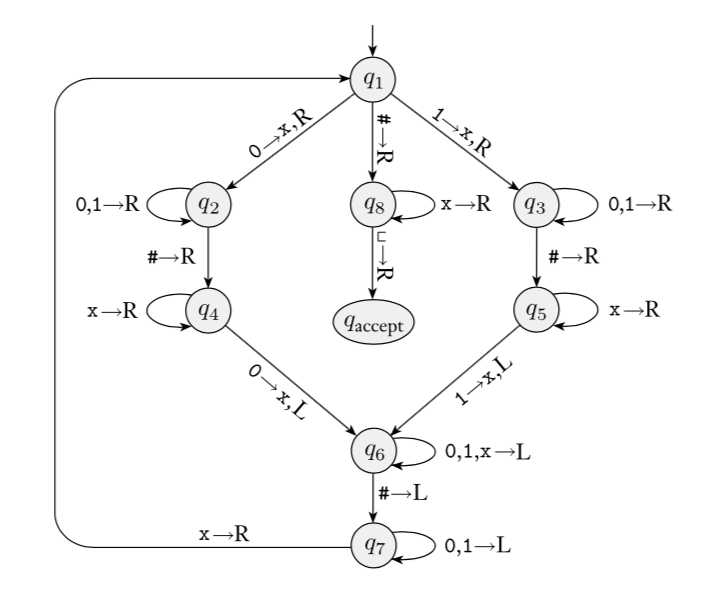
Sipser Figure 3.10
Conventions in state diagram of TM: \(b \to R\) label means \(b \to b, R\) and all arrows missing from diagram represent transitions with output \((q_{reject}, \textvisiblespace , R)\)
2
Implementation level description of this machine:
Zig-zag across tape to corresponding positions on either side of \(\#\) to check whether the characters in these positions agree. If they do not, or if there is no \(\#\), reject. If they do, cross them off.
Once all symbols to the left of the \(\#\) are crossed off, check for any un-crossed-off symbols to the right of \(\#\); if there are any, reject; if there aren’t, accept.
The language recognized by this machine is \[\{ w \# w \mid w \in \{0,1\}^* \}\]
Computation on input string \(01\#01\)
| \(q_1 \downarrow\) | ||||||
|---|---|---|---|---|---|---|
| \(0\) | \(1\) | \(\#\) | \(0\) | \(1\) | \(\textvisiblespace\) | \(\textvisiblespace\) |
2 High-level description of this machine is
Recall: High-level descriptions of Turing machine algorithms are written as indented text within quotation marks. Stages of the algorithm are typically numbered consecutively. The first line specifies the input to the machine, which must be a string.
Extra practice
Computation on input string \(01\#1\)
| \(q_1\downarrow\) | ||||||
|---|---|---|---|---|---|---|
| \(0\) | \(1\) | \(\#\) | \(1\) | \(\textvisiblespace\) | \(\textvisiblespace\) | \(\textvisiblespace\) |
A language \(L\) is recognized by a Turing machine \(M\) means
A Turing machine \(M\) recognizes a language \(L\) means
A Turing machine \(M\) is a decider means
A language \(L\) is decided by a Turing machine \(M\) means
A Turing machine \(M\) decides a language \(L\) means
Fix \(\Sigma = \{0,1\}\), \(\Gamma = \{ 0, 1, \textvisiblespace\}\) for the Turing machines with the following state diagrams:
|
|
| Decider? Yes / No | Decider? Yes / No |
|
|
| Decider? Yes / No | Decider? Yes / No |
A Turing-recognizable language is a set of strings that is the language recognized by some Turing machine. We also say that such languages are recognizable.
A Turing-decidable language is a set of strings that is the language recognized by some decider. We also say that such languages are decidable.
An unrecognizable language is a language that is not Turing-recognizable.
An undecidable language is a language that is not Turing-decidable.
True or False: Any decidable language is also recognizable.
True or False: Any recognizable language is also decidable.
True or False: Any undecidable language is also unrecognizable.
True or False: Any unrecognizable language is also undecidable.
True or False: The class of Turing-decidable languages is closed under complementation.
Using formal definition:
Using high-level description:
Church-Turing Thesis (Sipser p. 183): The informal notion of algorithm is formalized completely and correctly by the formal definition of a Turing machine. In other words: all reasonably expressive models of computation are equally expressive with the standard Turing machine.
Definition: A language \(L\) over an alphabet \(\Sigma\) is called co-recognizable if its complement, defined as \(\Sigma^* \setminus L = \{ x \in \Sigma^* \mid x \notin L \}\), is Turing-recognizable.
Theorem (Sipser Theorem 4.22): A language is Turing-decidable if and only if both it and its complement are Turing-recognizable.
Proof, first direction: Suppose language \(L\) is Turing-decidable. WTS that both it and its complement are Turing-recognizable.
Proof, second direction: Suppose language \(L\) is Turing-recognizable, and so is its complement. WTS that \(L\) is Turing-decidable.
Notation: The complement of a set \(X\) is denoted with a superscript \(c\), \(X^c\), or an overline, \(\overline{X}\).
Claim: If two languages (over a fixed alphabet \(\Sigma\)) are Turing-decidable, then their union is as well.
Proof:
Claim: If two languages (over a fixed alphabet \(\Sigma\)) are Turing-recognizable, then their union is as well.
Proof:
The Church-Turing thesis posits that each algorithm can be implemented by some Turing machine.
Describing algorithms (Sipser p. 185) To define a Turing machine, we could give a
Formal definition: the \(7\)-tuple of parameters including set of states, input alphabet, tape alphabet, transition function, start state, accept state, and reject state. This is the low-level programming view that models the logic computation flow in a processor.
Implementation-level definition: English prose that describes the Turing machine head movements relative to contents of tape, and conditions for accepting / rejecting based on those contents. This level describes memory management and implementing data access with data structures.
Mention the tape or its contents (e.g. “Scan the tape from left to right until a blank is seen.”)
Mention the tape head (e.g. “Return the tape head to the left end of the tape.”)
High-level description of algorithm executed by Turing machine: description of algorithm (precise sequence of instructions), without implementation details of machine. High-level descriptions of Turing machine algorithms are written as indented text within quotation marks. Stages of the algorithm are typically numbered consecutively. The first line specifies the input to the machine, which must be a string.
Use other Turing machines as subroutines (e.g. “Run \(M\) on \(w\)”)
Build new machines from existing machines using previously shown results (e.g. “Given NFA \(A\) construct an NFA \(B\) such that \(L(B) = \overline{L(A)}\)”)
Use previously shown conversions and constructions (e.g. “Convert regular expression \(R\) to an NFA \(N\)”)
Formatted inputs to Turing machine algorithms
The input to a Turing machine is always a string. The format of the input to a Turing machine can be checked to interpret this string as representing structured data (like a csv file, the formal definition of a DFA, another Turing machine, etc.)
This string may be the encoding of some object or list of objects.
Notation: \(\langle O \rangle\) is the string that encodes the object \(O\). \(\langle O_1, \ldots, O_n \rangle\) is the string that encodes the list of objects \(O_1, \ldots, O_n\).
Assumption: There are algorithms (Turing machines) that can be called as subroutines to decode the string representations of common objects and interact with these objects as intended (data structures). These algorithms are able to “type-check” and string representations for different data structures are unique.
For example, since there are algorithms to answer each of the following questions, by Church-Turing thesis, there is a Turing machine that accepts exactly those strings for which the answer to the question is “yes”
Does a string over \(\{0,1\}\) have even length?
Does a string over \(\{0,1\}\) encode a string of ASCII characters?1
Does a DFA have a specific number of states?
Do two NFAs have any state names in common?
Do two CFGs have the same start variable?
A computational problem is decidable iff language encoding its positive problem instances is decidable.
The computational problem “Does a specific DFA accept a given string?” is encoded by the language \[\begin{aligned} &\{ \textrm{representations of DFAs $M$ and strings $w$ such that $w \in L(M)$}\} \\ =& \{ \langle M, w \rangle \mid M \textrm{ is a DFA}, w \textrm{ is a string}, w \in L(M) \} \end{aligned}\]
The computational problem “Is the language generated by a CFG empty?” is encoded by the language \[\begin{aligned} &\{ \textrm{representations of CFGs $G$ such that $L(G) = \emptyset$}\} \\ =& \{ \langle G \rangle \mid G \textrm{ is a CFG}, L(G) = \emptyset \} \end{aligned}\]
The computational problem “Is the given Turing machine a decider?” is encoded by the language \[\begin{aligned} &\{ \textrm{representations of TMs $M$ such that $M$ halts on every input}\} \\ =& \{ \langle M \rangle \mid M \textrm{ is a TM and for each string } w, \textrm{$M$ halts on $w$} \} \end{aligned}\]
Note: writing down the language encoding a computational problem is only the first step in determining if it’s recognizable, decidable, or …
Deciding a computational problem means building / defining a Turing machine that recognizes the language encoding the computational problem, and that is a decider.
Some classes of computational problems will help us understand the differences between the machine models we’ve been studying. (Sipser Section 4.1)
| Acceptance problem | ||
| …for DFA | \(A_{DFA}\) | \(\{ \langle B,w \rangle \mid \text{$B$ is a DFA that accepts input string $w$}\}\) |
| …for NFA | \(A_{NFA}\) | \(\{ \langle B,w \rangle \mid \text{$B$ is a NFA that accepts input string $w$}\}\) |
| …for regular expressions | \(A_{REX}\) | \(\{ \langle R,w \rangle \mid \text{$R$ is a regular expression that generates input string $w$}\}\) |
| …for CFG | \(A_{CFG}\) | \(\{ \langle G,w \rangle \mid \text{$G$ is a context-free grammar that generates input string $w$}\}\) |
| …for PDA | \(A_{PDA}\) | \(\{ \langle B,w \rangle \mid \text{$B$ is a PDA that accepts input string $w$}\}\) |
| Language emptiness testing | ||
| …for DFA | \(E_{DFA}\) | \(\{ \langle A \rangle \mid \text{$A$ is a DFA and $L(A) = \emptyset$\}}\) |
| …for NFA | \(E_{NFA}\) | \(\{ \langle A\rangle \mid \text{$A$ is a NFA and $L(A) = \emptyset$\}}\) |
| …for regular expressions | \(E_{REX}\) | \(\{ \langle R \rangle \mid \text{$R$ is a regular expression and $L(R) = \emptyset$\}}\) |
| …for CFG | \(E_{CFG}\) | \(\{ \langle G \rangle \mid \text{$G$ is a context-free grammar and $L(G) = \emptyset$\}}\) |
| …for PDA | \(E_{PDA}\) | \(\{ \langle A \rangle \mid \text{$A$ is a PDA and $L(A) = \emptyset$\}}\) |
| Language equality testing | ||
| …for DFA | \(EQ_{DFA}\) | \(\{ \langle A, B \rangle \mid \text{$A$ and $B$ are DFAs and $L(A) =L(B)$\}}\) |
| …for NFA | \(EQ_{NFA}\) | \(\{ \langle A, B \rangle \mid \text{$A$ and $B$ are NFAs and $L(A) =L(B)$\}}\) |
| …for regular expressions | \(EQ_{REX}\) | \(\{ \langle R, R' \rangle \mid \text{$R$ and $R'$ are regular expressions and $L(R) =L(R')$\}}\) |
| …for CFG | \(EQ_{CFG}\) | \(\{ \langle G, G' \rangle \mid \text{$G$ and $G'$ are CFGs and $L(G) =L(G')$\}}\) |
| …for PDA | \(EQ_{PDA}\) | \(\{ \langle A, B \rangle \mid \text{$A$ and $B$ are PDAs and $L(A) =L(B)$\}}\) |
Example strings in \(A_{DFA}\)
Example strings in \(E_{DFA}\)
Example strings in \(EQ_{DFA}\)
\(M_1 =\) “On input \(\langle M,w\rangle\), where \(M\) is a DFA and \(w\) is a string:
Type check encoding to check input is correct type. If not, reject.
Simulate \(M\) on input \(w\) (by keeping track of states in \(M\), transition function of \(M\), etc.)
If the simulations ends in an accept state of \(M\), accept. If it ends in a non-accept state of \(M\), reject. "
What is \(L(M_1)\)?
Is \(M_1\) a decider?
Alternate description: Sometimes omit step 0 from listing and do implicit type check.
Synonyms: “Simulate”, “run”, “call”.
True / False: \(A_{REX} = A_{NFA} = A_{DFA}\)
True / False: \(A_{REX} \cap A_{NFA} = \emptyset\), \(A_{REX} \cap A_{DFA} = \emptyset\), \(A_{DFA} \cap A_{NFA} = \emptyset\)
A Turing machine that decides \(A_{NFA}\) is:
A Turing machine that decides \(A_{REX}\) is:
\(E_{DFA} = \{ \langle A \rangle \mid \text{$A$ is a DFA and $L(A) = \emptyset$}\}\). True/False: A Turing machine that decides \(E_{DFA}\) is
\(M_2 =\)“On input \(\langle M\rangle\) where \(M\) is a DFA,
For integer \(i = 1, 2, \ldots\)
Let \(s_i\) be the \(i\)th string over the alphabet of \(M\) (ordered in string order).
Run \(M\) on input \(s_i\).
If \(M\) accepts, \(\underline{\phantom{FILL IN BLANK}}\). If \(M\) rejects, increment \(i\) and keep going."
Choose the correct option to help fill in the blank so that \(M_2\) recognizes \(E_{DFA}\)
accepts
rejects
loop for ever
We can’t fill in the blank in any way to make this work
\(M_3 =\) “ On input \(\langle M \rangle\) where \(M\) is a DFA,
Mark the start state of \(M\).
Repeat until no new states get marked:
Loop over the states of \(M\).
Mark any unmarked state that has an incoming edge from a marked state.
If no accept state of \(A\) is marked, \(\underline{\phantom{FILL IN BLANK}}\); otherwise, \(\underline{\phantom{FILL IN BLANK}}\)".
To build a Turing machine that decides \(EQ_{DFA}\), notice that \[L_1 = L_2 \qquad\textrm{iff}\qquad (~(L_1 \cap \overline{L_2}) \cup (L_2 \cap \overline L_1)~) = \emptyset\] There are no elements that are in one set and not the other
\(M_{EQDFA} =\)
Summary: We can use the decision procedures (Turing machines) of decidable problems as subroutines in other algorithms. For example, we have subroutines for deciding each of \(A_{DFA}\), \(E_{DFA}\), \(EQ_{DFA}\). We can also use algorithms for known constructions as subroutines in other algorithms. For example, we have subroutines for: counting the number of states in a state diagram, counting the number of characters in an alphabet, converting DFA to a DFA recognizing the complement of the original language or a DFA recognizing the Kleene star of the original language, constructing a DFA or NFA from two DFA or NFA so that we have a machine recognizing the language of the union (or intersection, concatenation) of the languages of the original machines; converting regular expressions to equivalent DFA; converting DFA to equivalent regular expressions, etc.
Definition and Theorem: For an alphabet \(\Sigma\), a language \(L\) over \(\Sigma\) is called regular exactly when \(L\) is recognized by some DFA, which happens exactly when \(L\) is recognized by some NFA, and happens exactly when \(L\) is described by some regular expression
We saw that: The class of regular languages is closed under complementation, union, intersection, set-wise concatenation, and Kleene star.
Prove or Disprove: There is some alphabet \(\Sigma\) for which there is some language recognized by an NFA but not by any DFA.
Prove or Disprove: There is some alphabet \(\Sigma\) for which there is some finite language not described by any regular expression over \(\Sigma\).
Prove or Disprove: If a language is recognized by an NFA then the complement of this language is not recognized by any DFA.
Fix alphabet \(\Sigma\). Is every language \(L\) over \(\Sigma\) regular?
| Set | Cardinality |
|---|---|
| \(\{0,1\}\) | |
| \(\{0,1\}^*\) | |
| \(\mathcal{P}( \{0,1\})\) | |
| The set of all languages over \(\{0,1\}\) | |
| The set of all regular expressions over \(\{0,1\}\) | |
| The set of all regular languages over \(\{0,1\}\) | |
Strategy: Find an invariant property that is true of all regular languages. When analyzing a given language, if the invariant is not true about it, then the language is not regular.
Pumping Lemma (Sipser Theorem 1.70): If \(A\) is a regular language, then there is a number \(p\) (a pumping length) where, if \(s\) is any string in \(A\) of length at least \(p\), then \(s\) may be divided into three pieces, \(s = xyz\) such that
\(|y| > 0\)
for each \(i \geq 0\), \(xy^i z \in A\)
\(|xy| \leq p\).
Proof illustration
True or False: A pumping length for \(A = \{ 0,1 \}^*\) is \(p = 5\).