For Monday, Example 5.26 (page 237).
For Wednesday, Theorem 5.30 (page 238) and skim section 3.2.
Friday: no class in observance of Thanksgiving holiday.
For Monday of Week 10: Definition 7.1 (page 276)
Clearly and unambiguously communicate computational ideas using appropriate formalism. Translate across levels of abstraction.
Give examples of sets that are regular, context-free, decidable, or recognizable (and prove that they are).
Define and explain computational problems, including \(A\)**, \(E\)**, \(EQ\)**, (for ** DFA or TM) and \(HALT_{TM}\)
Know, select and apply appropriate computing knowledge and problem-solving techniques. Reason about computation and systems.
Use mapping reduction to deduce the complexity of a language by comparing to the complexity of another.
Explain what it means for one problem to reduce to another
Define computable functions, and use them to give mapping reductions between computational problems
Build and analyze mapping reductions between computational problems
Classify the computational complexity of a set of strings by determining whether it is regular, context-free, decidable, or recognizable.
State, prove, and use theorems relating decidability, recognizability, and co-recognizability.
Prove that a language is decidable or recognizable by defining and analyzing a Turing machines with appropriate properties.
Describe several variants of Turing machines and informally explain why they are equally expressive.
Define an enumerator
Define nondeterministic Turing machines
Use high-level descriptions to define and trace machines (Turing machines and enumerators)
Apply dovetailing in high-level definitions of machines
Review Quiz 9 on PrairieLearn (http://us.prairielearn.com), complete by Sunday 12/1/2024
Recall definition: \(A\) is mapping reducible to \(B\) means there is a computable function \(f : \Sigma^* \to \Sigma^*\) such that for all strings \(x\) in \(\Sigma^*\), \[x \in A \qquad \qquad \text{if and only if} \qquad \qquad f(x) \in B.\] Notation: when \(A\) is mapping reducible to \(B\), we write \(A \leq_m B\).
Theorem (Sipser 5.23): If \(A \leq_m B\) and \(A\) is undecidable, then \(B\) is undecidable.
Last time we proved that \(A_{TM} \le_m HALT_{TM}\) where \[HALT_{TM} = \{ \langle M, w \rangle \mid \text{$M$ is a Turing machine, $w$ is a string, and $M$ halts on $w$} \}\] and since \(A_{TM}\) is undecidable, \(HALT_{TM}\) is also undecidable. The function witnessing the mapping reduction mapped strings in \(A_{TM}\) to strings in \(HALT_{TM}\) and strings not in \(A_{TM}\) to strings not in \(HALT_{TM}\) by changing encoded Turing machines to ones that had identical computations except looped instead of rejecting.
True or False: \(\overline{A_{TM}} \leq_m \overline{HALT_{TM}}\)
True or False: \(HALT_{TM} \leq_m A_{TM}\).
Proof: Need computable function \(F: \Sigma^* \to \Sigma^*\) such that \(x \in HALT_{TM}\) iff \(F(x) \in A_{TM}\). Define
\(F = ``\) On input \(x\),
Type-check whether \(x = \langle M, w \rangle\) for some TM \(M\) and string \(w\). If so, move to step 2; if not, output \(\langle \hspace{2in} \rangle\)
Construct the following machine \(M'_x\):
Output \(\langle M'_x , w\rangle\)."
Verifying correctness: (1) Is function well-defined and computable? (2) Does it have the translation property \(x \in HALT_{TM}\) iff its image is in \(A_{TM}\)?
| Input string | Output string |
|---|---|
| \(\langle M, w \rangle\) where \(M\) halts on \(w\) | |
| \(\langle M, w \rangle\) where \(M\) does not halt on \(w\) | |
| \(x\) not encoding any pair of TM and string | |
Theorem (Sipser 5.28): If \(A \leq_m B\) and \(B\) is recognizable, then \(A\) is recognizable.
Proof:
Corollary: If \(A \leq_m B\) and \(A\) is unrecognizable, then \(B\) is unrecognizable.
Strategy:
(i) To prove that a recognizable language \(R\) is undecidable, prove that \(A_{TM} \leq_m R\).
(ii) To prove that a co-recognizable language \(U\) is undecidable, prove that \(\overline{A_{TM}} \leq_m U\), i.e. that \(A_{TM} \leq_m \overline{U}\).
\[E_{TM} = \{ \langle M \rangle \mid \text{$M$ is a Turing machine and $L(M) = \emptyset$} \}\]
Can we find algorithms to recognize
\(E_{TM}\) ?
\(\overline{E_{TM}}\) ?
Claim: \(A_{TM} \leq_m \overline{E_{TM}}\). And hence also \(\overline{A_{TM}} \leq_m E_{TM}\)
Proof: Need computable function \(F: \Sigma^* \to \Sigma^*\) such that \(x \in A_{TM}\) iff \(F(x) \notin E_{TM}\). Define
\(F = ``\) On input \(x\),
Type-check whether \(x = \langle M, w \rangle\) for some TM \(M\) and string \(w\). If so, move to step 2; if not, output \(\langle \hspace{2in} \rangle\)
Construct the following machine \(M'_x\):
Output \(\langle M'_x \rangle\)."
Verifying correctness: (1) Is function well-defined and computable? (2) Does it have the translation property \(x \in A_{TM}\) iff its image is not in \(E_{TM}\) ?
| Input string | Output string |
|---|---|
| \(\langle M, w \rangle\) where \(w \in L(M)\) | |
| \(\langle M, w \rangle\) where \(w \notin L(M)\) | |
| \(x\) not encoding any pair of TM and string | |
Recall: \(A\) is mapping reducible to \(B\), written \(A \leq_m B\), means there is a computable function \(f : \Sigma^* \to \Sigma^*\) such that for all strings \(x\) in \(\Sigma^*\), \[x \in A \qquad \qquad \text{if and only if} \qquad \qquad f(x) \in B.\]
So far:
\(A_{TM}\) is recognizable, undecidable, and not-co-recognizable.
\(\overline{A_{TM}}\) is unrecognizable, undecidable, and co-recognizable.
\(HALT_{TM}\) is recognizable, undecidable, and not-co-recognizable.
\(\overline{HALT_{TM}}\) is unrecognizable, undecidable, and co-recognizable.
\(E_{TM}\) is unrecognizable, undecidable, and co-recognizable.
\(\overline{E_{TM}}\) is recognizable, undecidable, and not-co-recognizable.
\[EQ_{TM} = \{ \langle M_1, M_2 \rangle \mid \text{$M_1$ and $M_2$ are both Turing machines and $L(M_1) =L(M_2)$} \}\]
Can we find algorithms to recognize
\(EQ_{TM}\) ?
\(\overline{EQ_{TM}}\) ?
Goal: Show that \(EQ_{TM}\) is not recognizable and that \(\overline{EQ_{TM}}\) is not recognizable.
Using Corollary to Theorem 5.28: If \(A \leq_m B\) and \(A\) is unrecognizable, then \(B\) is unrecognizable, it’s enough to prove that
\(\overline{HALT_{TM}} \leq_m EQ_{TM}\) aka \(HALT_{TM} \leq_m \overline{EQ_{TM}}\)
\(\overline{HALT_{TM}} \leq_m \overline{EQ_{TM}}\) aka \(HALT_{TM} \leq_m EQ_{TM}\)
Need computable function \(F_1: \Sigma^* \to \Sigma^*\) such that \(x \in HALT_{TM}\) iff \(F_1(x) \notin EQ_{TM}\).
Strategy:
Map strings \(\langle M, w \rangle\) to strings \(\langle M'_{x}, \scalebox{0.5}{\begin{tikzpicture}[->,>=stealth',shorten >=1pt, auto, node distance=2cm, semithick] \tikzstyle{every state}=[text=black, fill=none] \node[initial,state] (q0) {$q_0$}; \node[state,accepting] (qacc) [right of = q0, xshift = 20]{$q_{acc}$}; \path (q0) edge [loop above] node {$0, 1, \scalebox{1.5}{\textvisiblespace} \to R$} (q0) ; \end{tikzpicture}} \rangle\) . This image string is not in \(EQ_{TM}\) when \(L(M'_x) \neq \emptyset\).
We will build \(M'_x\) so that \(L(M'_{x}) = \Sigma^*\) when \(M\) halts on \(w\) and \(L(M'_x) = \emptyset\) when \(M\) loops on \(w\).
Thus: when \(\langle M,w \rangle \in HALT_{TM}\) it gets mapped to a string not in \(EQ_{TM}\) and when \(\langle M,w \rangle \notin HALT_{TM}\) it gets mapped to a string that is in \(EQ_{TM}\).
Define
\(F_1 = ``\) On input \(x\),
Type-check whether \(x = \langle M, w \rangle\) for some TM \(M\) and string \(w\). If so, move to step 2; if not, output \(\langle \hspace{2in} \rangle\)
Construct the following machine \(M'_x\):
Output \(\langle M'_{x}, \scalebox{0.5}{\begin{tikzpicture}[->,>=stealth',shorten >=1pt, auto, node distance=2cm, semithick] \tikzstyle{every state}=[text=black, fill=none] \node[initial,state] (q0) {$q_0$}; \node[state,accepting] (qacc) [right of = q0, xshift = 20]{$q_{acc}$}; \path (q0) edge [loop above] node {$0, 1, \scalebox{1.5}{\textvisiblespace} \to R$} (q0) ; \end{tikzpicture}} \rangle\) "
Verifying correctness: (1) Is function well-defined and computable? (2) Does it have the translation property \(x \in HALT_{TM}\) iff its image is not in \(EQ_{TM}\) ?
| Input string | Output string |
|---|---|
| \(\langle M, w \rangle\) where \(M\) halts on \(w\) | |
| \(\langle M, w \rangle\) where \(M\) loops on \(w\) | |
| \(x\) not encoding any pair of TM and string | |
Conclude: \(HALT_{TM} \leq_m \overline{EQ_{TM}}\)
Need computable function \(F_2: \Sigma^* \to \Sigma^*\) such that \(x \in HALT_{TM}\) iff \(F_2(x) \in EQ_{TM}\).
Strategy:
Map strings \(\langle M, w \rangle\) to strings \(\langle M'_{x}, \scalebox{0.5}{\begin{tikzpicture}[->,>=stealth',shorten >=1pt, auto, node distance=2cm, semithick] \tikzstyle{every state}=[text=black, fill=none] \node[initial,state,accepting] (q0) {$q_0$}; ; \end{tikzpicture}} \rangle\) . This image string is in \(EQ_{TM}\) when \(L(M'_x) = \Sigma^*\).
We will build \(M'_x\) so that \(L(M'_{x}) = \Sigma^*\) when \(M\) halts on \(w\) and \(L(M'_x) = \emptyset\) when \(M\) loops on \(w\).
Thus: when \(\langle M,w \rangle \in HALT_{TM}\) it gets mapped to a string in \(EQ_{TM}\) and when \(\langle M,w \rangle \notin HALT_{TM}\) it gets mapped to a string that is not in \(EQ_{TM}\).
Define
\(F_2 = ``\) On input \(x\),
Type-check whether \(x = \langle M, w \rangle\) for some TM \(M\) and string \(w\). If so, move to step 2; if not, output \(\langle \hspace{2in} \rangle\)
Construct the following machine \(M'_x\):
Output \(\langle M'_{x}, \scalebox{0.5}{\begin{tikzpicture}[->,>=stealth',shorten >=1pt, auto, node distance=2cm, semithick] \tikzstyle{every state}=[text=black, fill=none] \node[initial,state,accepting] (q0) {$q_0$}; ; \end{tikzpicture}} \rangle\) "
Verifying correctness: (1) Is function well-defined and computable? (2) Does it have the translation property \(x \in HALT_{TM}\) iff its image is in \(EQ_{TM}\) ?
| Input string | Output string |
|---|---|
| \(\langle M, w \rangle\) where \(M\) halts on \(w\) | |
| \(\langle M, w \rangle\) where \(M\) loops on \(w\) | |
| \(x\) not encoding any pair of TM and string | |
Conclude: \(HALT_{TM} \leq_m EQ_{TM}\)
Two models of computation are called equally expressive when every language recognizable with the first model is recognizable with the second, and vice versa.
Church-Turing Thesis (Sipser p. 183): The informal notion of algorithm is formalized completely and correctly by the formal definition of a Turing machine. In other words: all reasonably expressive models of computation are equally expressive with the standard Turing machine.
Some examples of models that are equally expressive with deterministic Turing machines:
The May-stay machine model is the same as the usual Turing machine model, except that on each transition, the tape head may move L, move R, or Stay.
Formally: \((Q, \Sigma, \Gamma, \delta, q_0, q_{accept}, q_{reject})\) where \[\delta: Q \times \Gamma \to Q \times \Gamma \times \{L, R, S\}\]
Claim: Turing machines and May-stay machines are equally expressive. To prove …
To translate a standard TM to a may-stay machine: never use the direction \(S\)!
To translate one of the may-stay machines to standard TM: any time TM would Stay, move right then left.
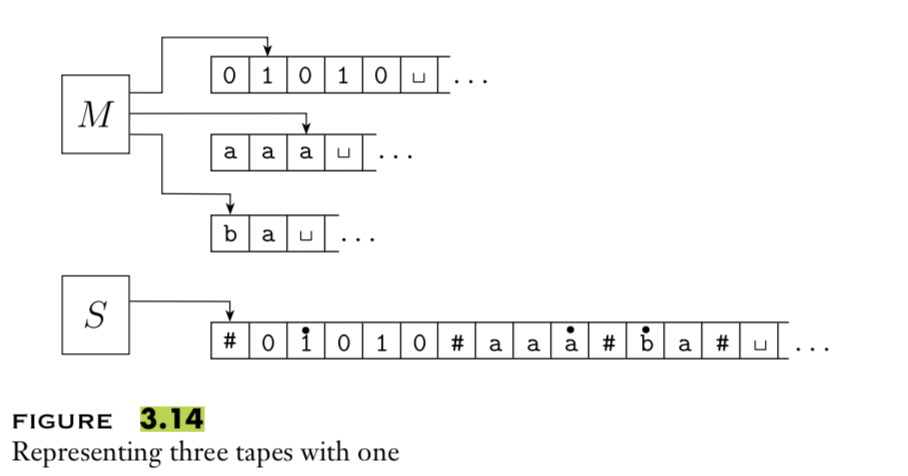
A multitape Turing macihne with \(k\) tapes can be formally representated as \((Q, \Sigma, \Gamma, \delta, q_0, q_{acc}, q_{rej})\) where \(Q\) is the finite set of states, \(\Sigma\) is the input alphabet with \(\textvisiblespace \notin \Sigma\), \(\Gamma\) is the tape alphabet with \(\Sigma \subsetneq \Gamma\) , \(\delta: Q\times \Gamma^k\to Q \times \Gamma^k \times \{L,R\}^k\) (where \(k\) is the number of states)
If \(M\) is a standard TM, it is a \(1\)-tape machine.
To translate a \(k\)-tape machine to a standard TM: Use a new symbol to separate the contents of each tape and keep track of location of head with special version of each tape symbol. Sipser Theorem 3.13
Enumerators give a different model of computation where a language is produced, one string at a time, rather than recognized by accepting (or not) individual strings.
Each enumerator machine has finite state control, unlimited work tape, and a printer. The computation proceeds according to transition function; at any point machine may “send” a string to the printer. \[E = (Q, \Sigma, \Gamma, \delta, q_0, q_{print})\] \(Q\) is the finite set of states, \(\Sigma\) is the output alphabet, \(\Gamma\) is the tape alphabet (\(\Sigma \subsetneq\Gamma, \textvisiblespace \in \Gamma \setminus \Sigma\)), \[\delta: Q \times \Gamma \times \Gamma \to Q \times \Gamma \times \Gamma \times \{L, R\} \times \{L, R\}\] where in state \(q\), when the working tape is scanning character \(x\) and the printer tape is scanning character \(y\), \(\delta( (q,x,y) ) = (q', x', y', d_w, d_p)\) means transition to control state \(q'\), write \(x'\) on the working tape, write \(y'\) on the printer tape, move in direction \(d_w\) on the working tape, and move in direction \(d_p\) on the printer tape. The computation starts in \(q_0\) and each time the computation enters \(q_{print}\) the string from the leftmost edge of the printer tape to the first blank cell is considered to be printed.
The language enumerated by \(E\), \(L(E)\), is \(\{ w \in \Sigma^* \mid \text{$E$ eventually, at finite time, prints $w$} \}\).
Theorem 3.21 A language is Turing-recognizable iff some enumerator enumerates it.
Proof, part 1: Assume \(L\) is enumerated by some enumerator, \(E\), so \(L = L(E)\). We’ll use \(E\) in a subroutine within a high-level description of a new Turing machine that we will build to recognize \(L\).
Goal: build Turing machine \(M_E\) with \(L(M_E) = L(E)\).
Define \(M_E\) as follows: \(M_E =\) “On input \(w\),
Run \(E\). For each string \(x\) printed by \(E\).
Check if \(x = w\). If so, accept (and halt); otherwise, continue."
Proof, part 2: Assume \(L\) is Turing-recognizable and there is a Turing machine \(M\) with \(L = L(M)\). We’ll use \(M\) in a subroutine within a high-level description of an enumerator that we will build to enumerate \(L\).
Goal: build enumerator \(E_M\) with \(L(E_M) = L(M)\).
Idea: check each string in turn to see if it is in \(L\).
How? Run computation of \(M\) on each string. But: need to be careful about computations that don’t halt.
Recall String order for \(\Sigma = \{0,1\}\): \(s_1 = \varepsilon\), \(s_2 = 0\), \(s_3 = 1\), \(s_4 = 00\), \(s_5 = 01\), \(s_6 = 10\), \(s_7 = 11\), \(s_8 = 000\), …
Define \(E_M\) as follows: \(E_{M} =\) “ ignore any input. Repeat the following for \(i=1, 2, 3, \ldots\)
Run the computations of \(M\) on \(s_1\), \(s_2\), …, \(s_i\) for (at most) \(i\) steps each
For each of these \(i\) computations that accept during the (at most) \(i\) steps, print out the accepted string."
At any point in the computation, the nondeterministic machine may proceed according to several possibilities: \((Q, \Sigma, \Gamma, \delta, q_0, q_{acc}, q_{rej})\) where \[\delta: Q \times \Gamma \to \mathcal{P}(Q \times \Gamma \times \{L, R\})\] The computation of a nondeterministic Turing machine is a tree with branching when the next step of the computation has multiple possibilities. A nondeterministic Turing machine accepts a string exactly when some branch of the computation tree enters the accept state.
Given a nondeterministic machine, we can use a \(3\)-tape Turing machine to simulate it by doing a breadth-first search of computation tree: one tape is “read-only” input tape, one tape simulates the tape of the nondeterministic computation, and one tape tracks nondeterministic branching. Sipser page 178
Summary
Two models of computation are called equally expressive when every language recognizable with the first model is recognizable with the second, and vice versa.
To prove the existence of a Turing machine that decides / recognizes some language, it’s enough to construct an example using any of the equally expressive models.
But: some of the performance properties of these models are not equivalent.