Week 6 at a glance
Textbook reading:
Chapter 3
Before Monday, Page 165-166 Introduction to Section 3.1.
Before Wednesday, Example 3.9 on page 173.
Before Friday, Page 184-185 Terminology for describing Turing
machines.
For Week 7 Monday: Introduction to Chapter 4.
We
will be learning and practicing to:
Clearly and unambiguously communicate computational ideas using
appropriate formalism. Translate across levels of abstraction.
Use precise notation to formally define the state diagram of a
Turing machine
Use clear English to describe computations of Turing machines
informally.
Motivate the definition of a Turing
machine
Trace the computation of a Turing machine on given
input
Describe the language recognized by a Turing
machine
Determine if a Turing machine is a
decider
Given an implementation-level description of a
Turing machine
Use high-level descriptions to define and trace
Turing machines
Apply dovetailing in high-level definitions of
machines
Give examples of sets that are recognizable and decidable (and
prove that they are).
State the definition of the class of recognizable
languages
State the definition of the class of decidable
languages
State the definition of the class of
co-recognizable languages
Know, select and apply appropriate computing knowledge and
problem-solving techniques. Reason about computation and
systems.
Describe and prove closure properties of classes of languages
under certain operations.
Apply a general construction to create a new Turing
machine from an example one.
Formalize a general construction from an informal
description of it.
Use general constructions to prove closure
properties of the class of decidable
langugages.
Use general constructions to prove closure
properties of the class of recognizable
langugages.
TODO:
This week: Test 1 Attempt 1 in CBTF.
Review Quiz 5 on PrairieLearn (http://us.prairielearn.com), due
2/12/2025
Mid quarter feedback survey on Canvas.
Monday: Descriptions of
Turing machines
We are ready to introduce a formal model that will capture a notion
of general purpose computation.
Similar to DFA, NFA, PDA: input will be an
arbitrary string over a fixed alphabet.
Different from NFA, PDA: machine is
deterministic.
Different from DFA, NFA, PDA: read-write
head can move both to the left and to the right, and can extend to the
right past the original input.
Similar to DFA, NFA, PDA: transition
function drives computation one step at a time by moving within a finite
set of states, always starting at designated start state.
Different from DFA, NFA, PDA: the special
states for rejecting and accepting take effect immediately.
(See more details: Sipser p. 166)
Formally: a Turing machine is \(M= (Q,
\Sigma, \Gamma, \delta, q_0, q_{accept}, q_{reject})\) where
\(\delta\) is the
transition function \[\delta: Q\times \Gamma \to Q \times \Gamma \times
\{L, R\}\] The computation of \(M\) on a string \(w\) over \(\Sigma\) is:
Read/write head starts at leftmost position on tape.
Input string is written on \(|w|\)-many leftmost cells of tape, rest of
the tape cells have the blank symbol. Tape
alphabet is \(\Gamma\)
with \(\textvisiblespace\in \Gamma\)
and \(\Sigma \subseteq \Gamma\). The
blank symbol \(\textvisiblespace \notin
\Sigma\).
Given current state of machine and current symbol being read at
the tape head, the machine transitions to next state, writes a symbol to
the current position of the tape head (overwriting existing symbol), and
moves the tape head L or R (if possible).
Computation ends if and when
machine enters either the accept or the reject state. This is called
halting. Note: \(q_{accept} \neq q_{reject}\).
The language recognized by the Turing
machine \(M\), is \(L(M) = \{ w \in \Sigma^* \mid w \textrm{ is
accepted by } M\}\), which is defined as \[\{ w \in \Sigma^* \mid \textrm{computation of $M$
on $w$ halts after entering the accept state}\}\]
2
Formal definition:
Sample computation:
| \(q0\downarrow\) |
|
| \(0\) |
\(0\) |
\(0\) |
\(\textvisiblespace\) |
\(\textvisiblespace\) |
\(\textvisiblespace\) |
\(\textvisiblespace\) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The language recognized by this machine is …
Describing Turing machines (Sipser p.
185) To define a Turing machine, we could give a
Formal definition: the \(7\)-tuple of parameters including set of
states, input alphabet, tape alphabet, transition function, start state,
accept state, and reject state; or,
Implementation-level definition:
English prose that describes the Turing machine head movements relative
to contents of tape, and conditions for accepting / rejecting based on
those contents.
High-level description: description
of algorithm (precise sequence of instructions), without implementation
details of machine. As part of this description, can “call" and run
another TM as a subroutine.
Fix \(\Sigma = \{0,1\}\), \(\Gamma = \{ 0, 1, \textvisiblespace\}\) for
the Turing machines with the following state diagrams:
Example of string accepted:
Example of string rejected:
Implementation-level description
High-level description
Example of string accepted:
Example of string rejected:
Implementation-level description
High-level description
Example of string accepted:
Example of string rejected:
Implementation-level description
High-level description
Example of string accepted:
Example of string rejected:
Implementation-level description
High-level description
Wednesday:
Recognizable and decidable languages
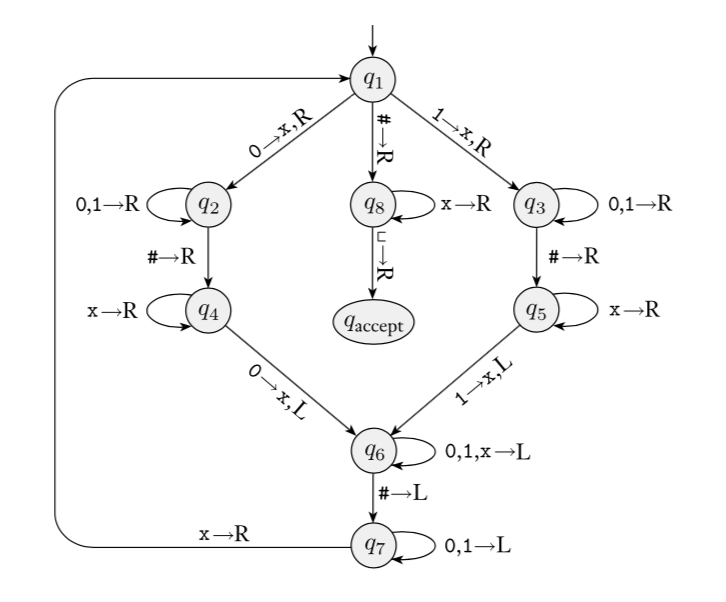
Sipser Figure 3.10
Conventions in state diagram of TM:
\(b \to R\) label means \(b \to b, R\) and all arrows missing from
diagram represent transitions with output \((q_{reject}, \textvisiblespace , R)\)
2
Implementation level description of this machine:
Zig-zag across tape to corresponding positions on either side of
\(\#\) to check whether the characters
in these positions agree. If they do not, or if there is no \(\#\), reject. If they do, cross them
off.
Once all symbols to the left of the \(\#\) are crossed off, check for any
un-crossed-off symbols to the right of \(\#\); if there are any, reject; if there
aren’t, accept.
The language recognized by this machine is \[\{ w \# w \mid w \in \{0,1\}^* \}\]
Computation on input string \(01\#01\)
| \(q_1
\downarrow\) |
|
| \(0\) |
\(1\) |
\(\#\) |
\(0\) |
\(1\) |
\(\textvisiblespace\) |
\(\textvisiblespace\) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 High-level description of this machine is
Recall: High-level descriptions of Turing
machine algorithms are written as indented text within quotation marks.
Stages of the algorithm are typically numbered consecutively. The first
line specifies the input to the machine, which must be a string.
Extra practice
Computation on input string \(01\#1\)
| \(q_1\downarrow\) |
|
| \(0\) |
\(1\) |
\(\#\) |
\(1\) |
\(\textvisiblespace\) |
\(\textvisiblespace\) |
\(\textvisiblespace\) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A language \(L\) is
recognized by a Turing machine \(M\) means
A Turing machine \(M\)
recognizes a language \(L\) means
A Turing machine \(M\) is a
decider means
A language \(L\) is
decided by a Turing machine \(M\) means
A Turing machine \(M\)
decides a language \(L\) means
Fix \(\Sigma = \{0,1\}\), \(\Gamma = \{ 0, 1, \textvisiblespace\}\) for
the Turing machines with the following state diagrams:
|
|
| Decider? Yes / No |
Decider? Yes / No |
|
|
|
|
| Decider? Yes / No |
Decider? Yes / No |
|
|
Friday:
Closure for the classes of recognizable and decidable languages
A Turing-recognizable language is a set
of strings that is the language recognized by some Turing machine. We
also say that such languages are recognizable.
A Turing-decidable language is a set of
strings that is the language recognized by some decider. We also say
that such languages are decidable.
An unrecognizable language is a
language that is not Turing-recognizable.
An undecidable language is a language
that is not Turing-decidable.
True or
False: Any decidable language is also
recognizable.
True or
False: Any recognizable language is also
decidable.
True or
False: Any undecidable language is also
unrecognizable.
True or
False: Any unrecognizable language is also
undecidable.
True or
False: The class of Turing-decidable
languages is closed under complementation.
Using formal definition:
Using high-level description:
Church-Turing Thesis (Sipser p. 183):
The informal notion of algorithm is formalized completely and correctly
by the formal definition of a Turing machine. In other words: all
reasonably expressive models of computation are equally expressive with
the standard Turing machine.